In recently published work, we show how change analysis from near-continuous 3D time series improves by considering full temporal information. How can it be done? Using 4D objects-by-change!
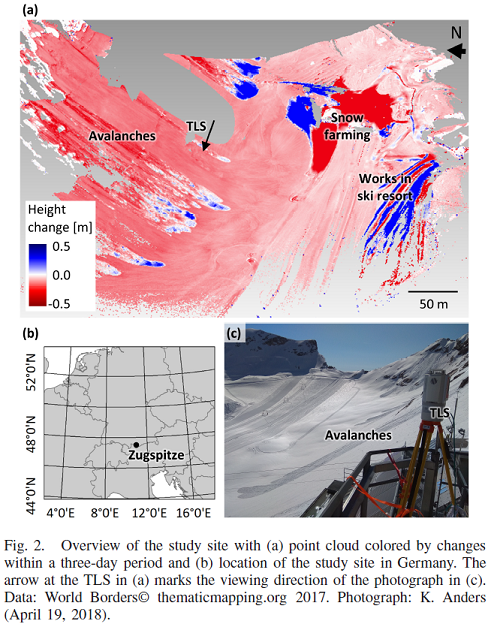
The method was applied to an hourly time series of terrestrial laser scans acquired for snow cover monitoring. In the snow-covered scene at the Zugspitze ski resort, all kinds of surface changes occurred with variable timing, duration, magnitudes, and so on – all a-priori unknown. The extraction of 4D objects-by-change detects different changes automatically and quantifies them more accurately than possible with standard, bitemporal change detection.
All details in the full paper:
Anders, K., Winiwarter, L., Höfle, B. (2022): Improving change analysis from near-continuous 3D time series by considering full temporal information. IEEE Geoscience and Remote Sensing Letters, 19. DOI: 10.1109/LGRS.2022.3148920
Source code and input data are openly available here:
Anders, K., Winiwarter, L., Höfle, B. (2021): Improving change analysis from near-continuous 3D time series by considering full temporal information [Data and Source Code]. heiDATA, V1. 10.11588/data/1L11SQ
Want to look into snow cover monitoring or test your own methods? We also published the full TLS time series open access, which was acquired during great field work at the environmental research station Schneefernerhaus (see this blogpost):
Anders, K., Eberlein, S., Höfle, B. (2022): Hourly Terrestrial Laser Scanning Point Clouds of Snow Cover in the Area of the Schneeferner, Zugspitze, Germany. PANGAEA. DOI: 10.1594/PANGAEA.941550
Snow cover monitoring at the Zugspitze is also featured in this video about our research on 4D change analysis:
Direct link to the video: https://youtu.be/Fdwq-Cp0mFY
This work was supported in part by the Top Researchers Fund of Heidelberg University and in part by the Heidelberg Graduate School of Mathematical and Computational Methods for the Sciences (HGS MathComp).