Statistical parameters often vary across geographic landscapes. For instance, when the the variance of georeferenced random variables is not stable, this might hint on variegated processes or contextual conditions in different sub-regions. Analysing such heterogeneous areas is challenging because an explicit consideration of this so-called spatial heterogeneity is required. Various approaches exist that take account of spatial heterogeneity. For instance, geographically weighted regression estimates local regression coefficients and adapted spatial hot-spot estimators like the O-statistic introduced by Keith Ord & Arthur Getis takes account of global structures when evaluating local conditions.
A related objective is the analysis of the heterogeneity itself, instead of taking account of it in the assessment of other statistical characteristics. This leads to the question of the role of the geographic arrangement ofspatial random variables for parameters such as the variance. The way how variables are situated in relation to each other in geographic space may either increase or decrease the variance, or it might have no effect at all. These insights would make an important contribution to a better characterization of the processes in different sub-regions.
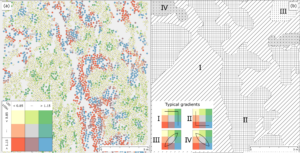
In a recent paper we put forward a novel statistical test called ‘Local Spatial Dispersion’ (LSD) that allows to draw inference about relationships between the geographic arrangement of random variables and their variance. The presented test relates spatially weighted local residuals with their randomized averages estimated from local contexts. Hypotheses about relationships are thereby only tested locally, without taking account of other parts of the analysed region. Because local subsets might become small quickly and because this can cause small-sample issues, a Bayesian estimation technique for generating additional synthetic local mean values is proposed. This ensures that Monte-Carlo randomizations can be carried out even in local subregions that are sparsely sampled.
Application of the method to a LiDAR-derived change dataset shows promising results. For example, it is possible to characterize a boundary between a mown and an unmown part of a meadow in detail, and to disclose haystacks and other features in other sub-regions. Our experiments also show little correlation of the proposed technique with the general level of variability. This means that the technique is driven by the influence of spatial pattern on the variance, as it is intended. Further, our results suggest that there is only a negligible relationship with Moran’s I, an estimator of spatial autocorrelation, which shows that our proposed method is able to reveal additional structures in datasets.
Westerholt, R., Resch, B., Mocnik, F.-B., and Hoffmeister, D. (2017): A statistical test on the local effects of spatially structured variance. International Journal of Geographical Information Science, volume and issue pending, pp. pending. DOI: 10.1080/13658816.2017.1402914.